摘要:通过采用有限元软件对薄壁方钢管梁柱加腋节点进行数值模拟,分析该节点的性能以及该节点的破坏模式。结果表明:该节点属于半刚性节点,不能简单的视为刚性连接或铰接;并且加劲肋应力变化较大,设计
摘 要:通过采用有限元软件对薄壁方钢管梁柱加腋节点进行数值模拟,分析该节点的性能以及该节点的破坏模式。结果表明:该节点属于半刚性节点,不能简单的视为刚性连接或铰接;并且加劲肋应力变化较大,设计时应具有足够的厚度;该节点的最终破坏是由于方钢管梁的局部屈曲,符合“强节点弱杆件”的抗震设计原则。
关键词:薄壁方钢管;加腋节点;半刚性连接;数值模拟
1前 言
薄壁轻钢结构作为一种新型的钢结构体系,由于薄壁轻钢结构具有整体性好、高次超静定的结构体系,具有多道抗震防线的优点,并且符合我国的环保、节能、节水、住宅产业化政策,将成为我国建筑发展的新趋势[1]。在我国薄壁轻钢结构房屋体系(图1)当中,其轻钢骨架梁柱构件通常采用冷弯薄壁方钢管、矩形钢管、C型钢、L型钢、槽型钢,然而在这些截面形式当中,以方钢管、矩形钢管的截面形式较优越。这类截面材料绕中和轴均匀分布,使得截面具有良好的抗压和抗弯扭承载能力以及较大的刚度[2],从而降低结构的用钢量。然而在这类轻钢骨架之间通常采用直接焊接方式(图2),采用焊接方式连接,密闭性好,板件净截面面积不会减小,但在这种节点反复焊接过程当中,对节点部分产生很明显的初始应力,节点脆性明显增

图1 轻钢结构骨架体系(薄壁方钢管梁柱加腋节点)
加,降低节点的延性,然而节点是构成钢框架不可
缺少的部分,并且历次地震,如1985年墨西哥城地震、1994年美国诺斯里齐地震、1995年日本阪神地震,大部分轻钢建筑都以节点的破坏而导致建筑的倒塌,因此对这类轻钢结构的节点连接应受到工程界的广泛重视[3-4]。为此本文提出在方钢管梁的上下翼缘增设加劲肋,以改善节点的强度和刚度。建立三维空间节点有限元模型进行分析,探讨加腋后节点的性能及其破坏模式。
2.模型建立
2.1几何模型
图3为本文研究节点的三维视图,其中方钢管柱的截面尺寸为120×120×3mm,高度为1200mm,两个方钢管柱之间间距为600mm;方钢管梁1、2截面尺寸为100×100×2mm,其中方钢管梁1长度700mm,方钢管梁2长度为480mm;加劲板尺寸为120×50×3mm,加劲肋尺寸为40×3mm。

图2现场焊接节点(薄壁方钢管梁柱加腋节点)
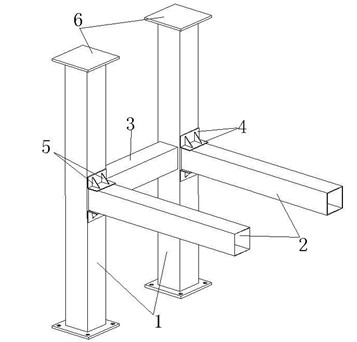
(1-方钢管柱,2-方钢管梁1,3-方钢管梁2,
4-加劲板,5-加劲肋,6-方钢管柱底板)
图3 加腋节点三维视图
2.2 材料模型
方钢管梁柱的材料特性见图5,加劲肋与梁柱所用材料相同,故取相同值。采用多线性材料模型,弹性模量E=161249.7MPa,泊松比ν=0.3。模型采用的屈服准则为Von Mises屈服准则,并且认为材料是各向同性强化的。
2.3有限元模型
采用ANSYS软件对图3所示的连接节点建立有限元计算模型。由于方钢管梁柱的长度及宽度与其壁厚的比值较大,故采用每个节点具有6个自由度的壳单元shell181,该单元具有应力刚化及大变形功能,具有强大的非线性功能;增设的加劲肋采用四面体单元solid92,每个节点具有三个自由度,该单元支持塑性、蠕动、膨胀、应力钢化、大变形和大张力;方钢管柱上下底板采用solid45单元,并且假定其为刚性;在方钢管梁1端部增加端板,其中线距离方钢管柱翼缘距离为650mm,假定其为刚性。对于体单元与壳单元的公共边界采用共用节点,建立该节点的有限元模型如图4所示,并对节点域处的单元网格划分加密。方钢管柱底部为固端上部为铰接的边界条件。
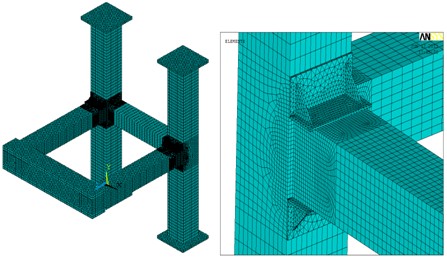
图4 加腋节点有限元模型(薄壁方钢管梁柱加腋节点)
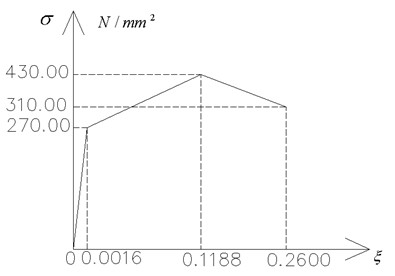
图5材料本构
3.计算结果分析
3.1荷载位移曲线
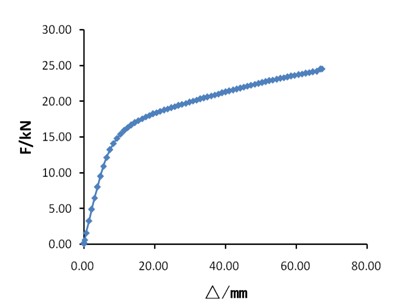
图6 荷载位移曲线(薄壁方钢管梁柱加腋节点)
图6为该节点的荷载位移曲线,该节点在开始处于弹性阶段,荷载与位移呈线性增加,当荷载达到13.23kN时,节点开始屈服,对应的屈服位移为7.4mm;随即进入屈服阶段,达到节点的极限承载力为25.53kN,按全截面塑性发展,可计算其极限承载力为26.33kN,略大于有限元计算结果。该节点的弯矩转角曲线与荷载位移曲线变化相似,同时可计算其初始转动刚度为847.5kN•m。
根据文献5当中连接的初始转动刚度Ki标准定义为: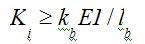 ,则为刚接;
,则为刚接;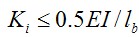 ,则为铰接;
,则为铰接; 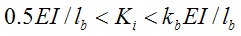 ,则为半刚性连接;
,则为半刚性连接;
E为钢材弹性模量,Ib为梁截面惯性矩,Lb为梁跨度,kb=8(有支撑框架)或kb=25(无支撑框架)。
可计算得:
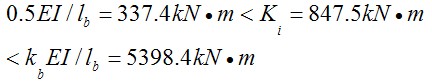 即属于半刚性连接。
即属于半刚性连接。
当以连接的受弯承载力为标准定义:该节点的塑性弯矩为 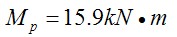 ;粱端的塑性转角:
;粱端的塑性转角: 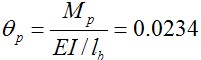 。其中取
。其中取  ,
,
 ,可得其相对弯矩转角曲线如图7所示,可见该节点的相对弯矩转角曲线位于半刚性连接区域类,并且与刚性连接或铰接连接均相差较大,因此在设计时不能简单的将该类节点视为刚接或铰接连接。
,可得其相对弯矩转角曲线如图7所示,可见该节点的相对弯矩转角曲线位于半刚性连接区域类,并且与刚性连接或铰接连接均相差较大,因此在设计时不能简单的将该类节点视为刚接或铰接连接。
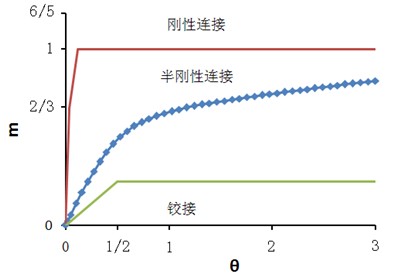
图7 相对弯矩转角曲线
3.2 应力分析
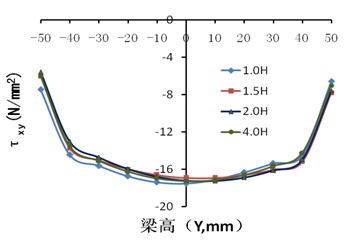
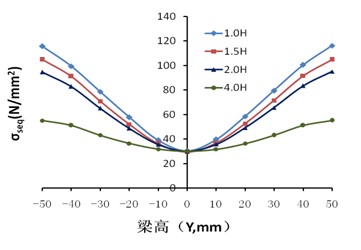
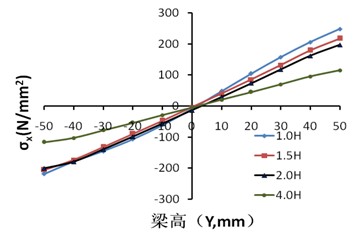
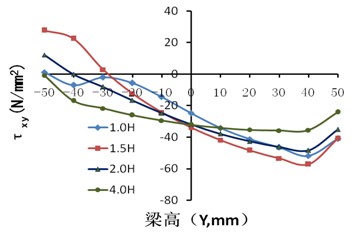
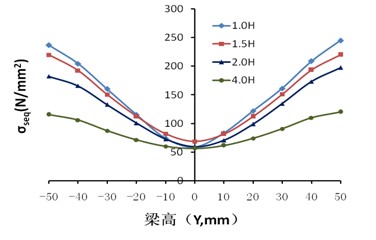
图8(弹性阶段)及图9(极限荷载作用时)为节点沿方钢管梁1长度方向各截面的应力发展趋势,1.0H、1.5H、2.0H、4.0H(梁形心与柱翼缘交点为坐标原点,X轴、Y轴和Z轴分别为梁宽方向、梁高方向、梁长方向,H为梁截面高度)。
从图8(a)可以看出梁的弯曲应力大致成三角形分布,剪应力大致呈抛物线分布,并且各截面处梁腹板的剪应力大致相等,均符合经典的梁理论。Mises应力分布大致也成抛物线型分布,但随着距离方钢管柱表面距离的减小,其应力变化更大。
(a)正应力分布
(b)剪应力分布
(c)Misses应力分布
图8 沿梁长度方向各截面的应力分布图
从图9(a)可以看出,正应力的分布与弹性节点变化相似,而剪应力与弹性阶段的明显不同,其原因主要是方钢管梁在进入屈服阶段过程中,剪应力发生了内力重分布。在X=1.0H时,腹板中部的Mises略大于其余部位,表面在继续承受荷载作用时,该部位率先发生屈曲。
图10为极限荷载作用下方钢管柱的Mises应力分布,从中可以看出,方钢管柱腹板应力大部分小于屈服应力,表明增设加劲肋能够明显改善在节点域柱腹板的应力,防止柱发生屈曲;图11为加劲肋与加劲板的Mises应力分布,在加劲肋的角部产生应力集中现象,局部应力已明显超过屈服应力,局部接近极限应力值,可见在设计时三角形加劲肋应具有足够的厚度,以防止应力集中而被拉裂。
(a)正应力分布
(b)剪应力分布
(c)Misses应力分布
图9 沿梁长度方向各截面的应力分布图
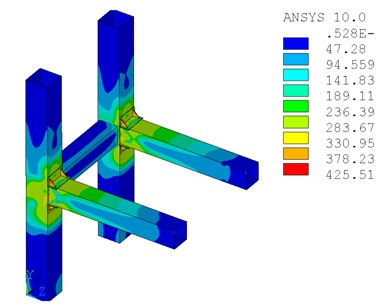
图10 方钢管柱的Mises应力分布
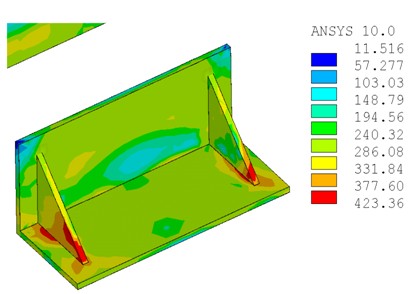
图11 三角形加劲肋的Mises应力分布
3.3破坏模式
节点在弹性工作状态下,荷载位移曲线为基本直线段,荷载随位移的增大而增长很快,此时连接刚度大,在节点进入屈服阶段之前,加劲肋的应力较大,此处也是最早出现塑性区,随着荷载的增加,节点整体荷载位移曲线开始弯曲。随着荷载的增大,角钢的塑性区不断扩大,刚度下降,加载点位移增加较快,但此时角钢并没出现较明显的屈曲。达到极限荷载后,加劲肋开始出现屈曲,不过此时节点域处方钢管梁应力增长较快,大部分进入塑性,同时腹板出现向外鼓曲,下翼缘向内凹陷(图12),其变形速度较加劲肋快许多,而此时方钢管柱的应力几乎没变,可见该节点符合“强柱弱梁”的设计原则。
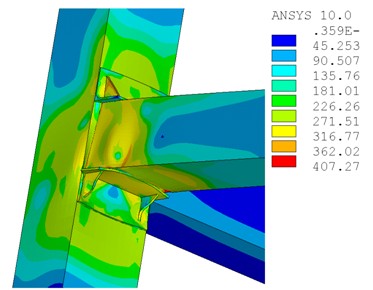
图12节点破坏模式
4.结 论
1)通过对该节点的荷载位移曲线以及节点的初始转动刚度大小的研究表明,该节点既不能简化成刚性连接,更不能视为铰接,而属于梁柱半刚性连接;
2)在外荷载作用下,增设加劲肋能明显改善节点域柱腹板的应力,并且节点的最终破坏模式是由于方钢管梁的局部屈曲,符合“强节点弱杆件”的设计原则。加劲肋的应力较大,设计时应具有足够的厚度,以满足“强节点弱杆件”的抗震设计原则。
参考文献
[1] 姚勇,褚云朋,邓勇军,等.低层冷弯薄壁型钢结构体系动静性能数值模拟[J].建筑结构.2011(2):41-45.
[2] 陈骥.钢结构稳定理论与设计[M].西安建筑科技大学.2005:242-298.
[3] 田俊杰.轻型钢结构体系节点半刚性连接性能及框架极限承载力分析[D].长沙理工大学硕士学位论文.2003.
[4] 陈坚.新型轻钢龙骨体系梁-柱节点试验性研究及有限元分析[D].武汉理工大学硕士学位论文.2006.
[5] 李国强,石文龙,王静峰.半刚性连接钢框架结构设计[M].中国建筑工业出版社.2009:1-2.
(西南科技大学土木工程与建筑学院)




